Las notaciones sirven de base para expresar sentencias bien definidas. El uso más extendido de las notaciones sirve para expresar operaciones aritméticas. Las expresiones aritméticas se pueden expresar de tres formas distintas:
La diversidad de notaciones corresponde en que para algunos casos es más sencillo un tipo de notación. También dependen de cómo se recorrerá el árbol sintáctico, el cual puede ser en in-orden, pre-orden o post-orden; teniendo una relación de uno a uno con la notación de los operadores.
Las notaciones son una forma especial en la que se pueden expresar una expresión
matemática y puedan ser de 3 formas: infija, prefija y posfija. Los prefijos, Pre - Pos - In se
refieren a la posición relativa del operador con respecto a los dos operandos.
2.1.1 Prefija
La expresión o notación prefija nos indica que el operador va antes de los
operandos sus características principales son:
- Los operadores conservan el mismo orden que la notación infija equivalente.
- No requiere de paréntesis para indicar el orden de precedencia de operadores
ya que él es una operación.
- Se evalúa de izquierda a derecha hasta que encuentra el primer operador
seguido inmediatamente de un par de operando.
- Se evalúa la expresión binaria y el resultado se cambia como un nuevo
operando. Se repite hasta que nos quede un solo resultado.
- El orden es operador, primer operando, segundo operando.
Conversión de infija a prefija:
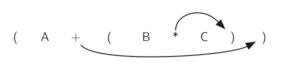
A + B * C se puede escribir como (A + (B * C ) ) para indicar claramente que la multiplicación tiene prioridad sobre la suma. Sin embargo, si se observa de cerca puede ver que cada par de corchetes también indica el comienzo y el final del par de operandos, con los operadores correspondientes en el medio.
Mire el paréntesis de cierre en la sub-expresión (B * C) anterior. Si movemos el símbolo de multiplicación a esa posición y eliminamos el paréntesis izquierdo correspondiente, obtenemos B C *, en realidad hemos convertido la sub-expresión en un símbolo de sufijo. Si el operador de suma también se mueve a su posición correspondiente del paréntesis derecho y se elimina el paréntesis izquierdo correspondiente, la expresión postfija completa se obtendrá de la siguiente manera:
2.1.2 Infija
La expresión o notación infija es la forma más común que utilizamos para escribir
expresiones matemáticas, estas notaciones se refiere a que el operador esta entre los
operadores. La notación infija puede estar completamente parentizada o puede basarse en
un esquema de precedencia de operadores así como el uso de paréntesis para invalidar los
arreglos al expresar el orden de evaluación de una expresión:
3*4 = 12 3*4+ = 14 3*(4+2) = 18
La notación infija tiene el problema de que en expresiones con más de un operador
existe ambigüedad sobre cuál es el orden de evaluación. Por ejemplo, la expresión 8/4/2 se
puede interpretar como (8/4)/2 o bien 8/(4/2). Las otras notaciones no sufren este problema.
*La notación habitual. El orden es primer operando, operador, segundo operando.*
2.1.3 Postfija
Como su nombre lo indica se refiere a que el operador ocupa la posición después de
los operandos sus características principales son:
- El orden de los operandos se conserva igual que la expresión infija equivalente
no utiliza paréntesis ya que no es una operación ambigua.
- La operación posfija no es exactamente lo inverso a la operación prefija
equivalente.
- El orden es primer operando, segundo operando, operando. (A+B)*C AB+C*
Ejemplo:
Si deseamos representar las expresiones (2+(3*4)) = x y ((2+3)*4) = x en las tres
notaciones mencionadas, el resultado sería:
(2+(3*4)) = x
((2+3)*4) = x
Notación postfija
2 3 4 * + x = 2 3 + 4 * x =
Autores:
- Gutiérrez de la Cruz Axel
- López Hernández Joseph Aldahir
Referencias
Josue, R. G. (2015). Unidad 2. Generación de Código
Intermedio. Tecnológico de Estudios Superiores de Cuautitlán Izcalli.
Recuperado el 8 de Marzo de 2022